Sobel Operator

The Sobel operator is at the heart of the Canny edge detection algorithm you used in the Introductory Lesson. Applying the Sobel operator to an image is a way of taking the derivative of the image in the x or y direction. The operators for Sobel_x and Sobel_y , respectively, look like this:

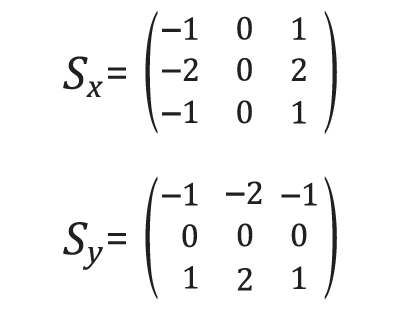
These are examples of Sobel operators with a kernel size of 3 (implying a 3 x 3 operator in each case). This is the minimum size, but the kernel size can be any odd number. A larger kernel implies taking the gradient over a larger region of the image, or, in other words, a smoother gradient.

To understand how these operators take the derivative, you can think of overlaying either one on a 3 x 3 region of an image. If the image is flat across that region (i.e., there is little change in values across the given region), then the result (summing the element-wise product of the operator and corresponding image pixels) will be zero.

For example, given:

The element-wise product would be:

In which case, the sum of this matrix is 0 , implying a flat gradient (in the x-direction in this calculation, although the y-direction is also zero in this example).

If, instead, for example, you apply the S_x operator to a region of the image where values are rising from left to right, then the result will be positive, implying a positive derivative.

Given:

The element-wise product would be:

This time, the sum of this matrix is 8 , meaning a gradient exists in the x-direction. Note that in this example image region, if you applied the S_y operator, the result would be a gradient of 0 in the y-direction, as the values are not varying from top to bottom.

Visual Example

If we apply the Sobel x and y operators to this image:

And then we take the absolute value, we get the result:

x vs. y

In the above images, you can see that the gradients taken in both the x and the y directions detect the lane lines and pick up other edges. Taking the gradient in the x direction emphasizes edges closer to vertical. Alternatively, taking the gradient in the y direction emphasizes edges closer to horizontal.

In the upcoming exercises, you'll write functions to take various thresholds of the x and y gradients. Here's some code that might be useful:

Examples of Useful Code

You need to pass a single color channel to the cv2.Sobel() function, so first convert it to grayscale:

gray = cv2.cvtColor(im, cv2.COLOR_RGB2GRAY)

** Note: ** Make sure you use the correct grayscale conversion depending on how you've read in your images. Use cv2.COLOR_RGB2GRAY if you've read in an image using mpimg.imread() . Use cv2.COLOR_BGR2GRAY if you've read in an image using cv2.imread() .

Calculate the derivative in the x direction (the 1, 0 at the end denotes x direction):

sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0)

Calculate the derivative in the y direction (the 0, 1 at the end denotes y direction):

sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1)

Calculate the absolute value of the x derivative:

abs_sobelx = np.absolute(sobelx)

Convert the absolute value image to 8-bit:

scaled_sobel = np.uint8(255*abs_sobelx/np.max(abs_sobelx))

** Note: ** It's not entirely necessary to convert to 8-bit (range from 0 to 255) but in practice, it can be useful in the event that you've written a function to apply a particular threshold, and you want it to work the same on input images of different scales, like jpg vs. png. You could just as well choose a different standard range of values, like 0 to 1 etc.

Create a binary threshold to select pixels based on gradient strength:

thresh_min = 20
thresh_max = 100
sxbinary = np.zeros_like(scaled_sobel)
sxbinary[(scaled_sobel >= thresh_min) & (scaled_sobel <= thresh_max)] = 1
plt.imshow(sxbinary, cmap='gray')

** Result **